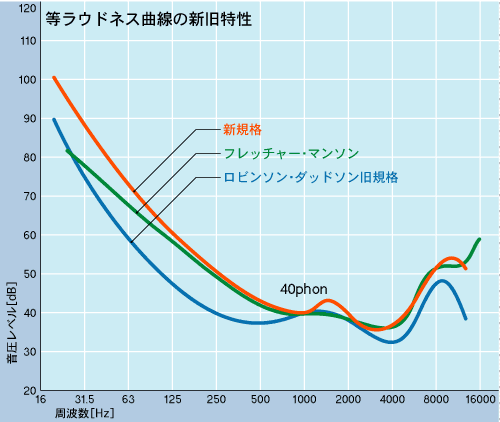
等ラウドネス曲線

人間の可聴領域は20Hzから20,000Hzと言われていますが、その中でも2,000Hzから4,000Hzの音が、感度がよく聞き取りやすい周波数帯となっています。感度がよいというのは同じ音でもより大きく聞こえるということです。例えば一定の音圧を用いて周波数だけ変化させると、3,000Hzでは大きく聞こえ、30Hzでは小さく聞こえます。同じ音圧（エネルギー）なのに何が変化しているのでしょうか？周波数を変えてもエネルギーは変化しません。この変化がラウドネスであり、30Hzの音を3,000Hzの音と同等の聞こえ（ラウドネス）にするには音圧を上げる必要があります。この人間の耳の感覚的な特性がラウドネスであり、それをグラフ化したものが等ラウドネス曲線になります。

例えは下の図で説明すると、周波数が1,000Hz、音圧レベルが40dBのときのラウドネス（聞こえる大きさ）を40phon（ホン）とします。このラウドネスを維持するように周波数を変化させると、音圧が大きく変わることがわかります。つまり低い周波数で同じラウドネス（聞こえる大きさ）にするには、大きな音圧が必要になるということです。方程式などで決まらずに人間の耳で測定した結果です。

話は変わりますが、不快な音といえば爪で黒板を引っかく音を想像します。面白いことに人間にとって最も不快な音も2,000Hz〜4,000Hzという研究報告があります。人間の外耳道の形と関係があり、この周波数帯の音が耳の中で増幅されやすいという特徴が原因と推測されています。ラウドネスを考えると感度がいいので、不快な音がより不快に聞こえるのかなとも思います。